GPS: subgoaling
Table of Contents
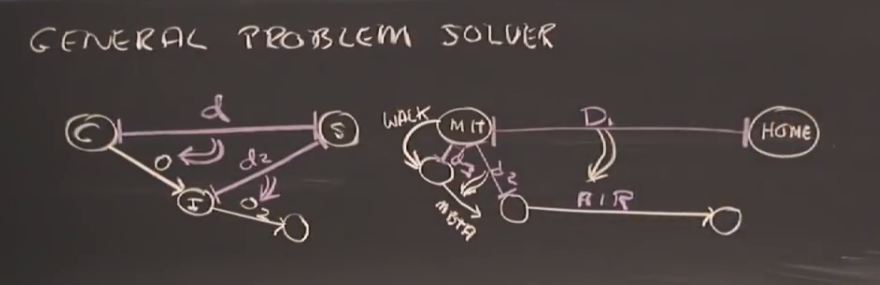 with the example on the right, with the distance between MIT and home \(d_1\), you decide that airplane is the best transportation method; but you can’t get on an plane from the classroom, so you had to solve the problem of going from MIT to airport, the difference/distance to which in here is denoted with \(d_2\)
with the example on the right, with the distance between MIT and home \(d_1\), you decide that airplane is the best transportation method; but you can’t get on an plane from the classroom, so you had to solve the problem of going from MIT to airport, the difference/distance to which in here is denoted with \(d_2\)
To go to airport, based on the distance \(d_2\), you decide that Metro is the best transportation method, but again there’s none in the class room ,so you have to find a way to get to the Metro station. The distance from classroom to Metro station is denoted \(d_3\)
Based on the distance \(d_3\), which is probably 500 meters, walking seems about just enough, so you choose to walk from classroom to metro station, and you can start walking from classroom. Problem Solved!
Backlinks
 Assume a current state \(C\) and goal state \(S\), define a difference/distance between the 2 states \(d\). With previously known operator \(o\), a transition can be made from \(C\) to an intermediate state \(I\).
Assume a current state \(C\) and goal state \(S\), define a difference/distance between the 2 states \(d\). With previously known operator \(o\), a transition can be made from \(C\) to an intermediate state \(I\).